Im Grundlagen-Fach behandeln wir gerade u. a. das Thema binäre Suchbäume, für das ich eine C++-Implementierung erstellen soll. Meine C++-Version war noch nicht ganz fertig, als mir die Idee kam es einmal mit Processing zu versuchen - der besondere Zweck dieses Entwicklungssystems liegt darin, etwas einfach und schnell zu visualisieren.
Früher bereits kam mir einmal die Idee Processing zu benutzen um das Prototyping zu forcieren bzw. Algorithmen einfach zu visualisieren und damit den Ablauf testen zu können (abseits vom Programmkontext) – leider war ich aber noch nicht dazu gekommen. Das hole ich hiermit nach.
Für das Prototyping speziell in C# - und nicht unbedingt Grafik-bezogen - kann aber auch der Snippet Compiler oder der sharpsnippetcompiler verwendet werden - empfohlen wird auch LINQPad für diesen Zweck, obwohl es ursprünglich nur für LINQ-Abfragen gedacht war.
Die Entwicklungsumgebung von Processing ist bewusst einfach gehalten, aber es gibt trotzdem eine Konsolenausgabe. Die Syntax der Befehle ist zu Java/C#/C++ weitgehend identisch (es basiert auf Java, ergänzt mit einfachen Zeichen- und Steuerungsbefehlen), leider gibt es keine automatische Befehlsvervollständigung. Interessant ist u. a., das das Syntax-Highlighting von Processing die Klein/Großschreibung ignoriert, der Compiler aber nicht.
Etwas gefährlich ist das es kein separates Fenster oder Tab für die Suchen & Ersetzen-Funktion gibt, denn wenn man nach so einer Aktion nur suchen will ersetzt man leicht aus Versehen etwas - da das Feld Replace with mit dem letzten Wert gefüllt bleibt.
Grundsätzlich gibt es bei Processing-Programmen keine Main-Funktion und es unterscheidet zwischen einem statischen und einem aktiven Modus. Der statische Modus ist gedacht für Programme die einzelne Bilder ohne weitere Interaktion erstellen, der aktive Modus für interaktive Programme.
Der statische Modus scheint eine Mischung aus der prozeduralen und der objektorientierten Programmierung zu sein (Oberbegriff: Imperative Programmierung) – eine Ablaufsteuerung ist nur ausgehend von selbst definierten Klassen möglich; das Implementieren von Funktionen ohne Klassenzugehörigkeit ist möglich, deren Aufruf aber nur aus Klassen heraus erlaubt. Ansonsten können Programmbefehle im statischen Modus quasi freistehend geschrieben werden (wie auch beispielsweise in VBScript), aber sobald man versucht von dort eine freistehende Funktion aufzurufen kommt (anders als in VBScript) die Fehlermeldung
It looks like you´re mixing “active” and “static” modes.
Im statischen Modus muss man demnach auf direkte Aufrufe eigener Funktionen (außerhalb von Klassen) verzichten. Im aktiven Modus hat man dagegen die komplette Ablaufsteuerung, dazu implementiert man z. B. einfach die Events setup() und draw(). Draw() wird eigentlich bei jedem Zeichnen eines Bildes aufgerufen, aber wenn der Befehl noLoop(); erfolgt kommt es nur zu einem einmaligen Aufruf dieses Events.
Ein Einstiegspunkt scheint formal nicht vorgeschrieben zu sein, setup() wird eigentlich nur für Initalisierungen empfohlen - aber wie gesagt, eine Main-Funktion gibt es nicht. Die Vorgehensweise ist so etwas gewöhnungsbedürftig, aber nicht weiter schwierig. Für einen genaueren Überblick verweise ich an dieser Stelle auf den Overview von Processing.
Nachfolgend meine erste funktionierende Implementierung eines binären Suchbaumes in Processing. Die Version ist aber nicht vollständig, denn es fehlen noch Routinen für Suche, Löschen etc. - jedoch geht es bei mir mit Processing nur um die Visualisierung, eine vollständige Version in C++ wird später noch folgen.
Ein binärer Suchbaum hat entweder keinen, einen oder zwei Nachfolger. Das der gesamte Teilbaum eines Knotens entweder kleiner oder größer als der Vaterknoten ist liegt nicht nur daran das kleinere Werte als linker und größere als rechter Sohn eingefügt werden, sondern auch daran, das jeder Knoten vom Wurzelknoten ausgehend in den Baum eingefügt wird - es erfolgen rekursive Aufrufe, wenn der aktuelle Knoten bereits den linken oder rechten Nachfolger hat (wie gesagt kann es maximal zwei Söhne geben).
Wieviele Ebenen für eine n-Anzahl an Knoten es geben kann unterscheidet sich in einem Minimum und einem Maximum. Das Maximum entspricht immer der Gesamtanzahl an Elementen, das Minimum berechnet sich nach der Formel ⌊log(2, n)⌋+1. Das Ergebnis des Logarithmus wird also abgerundet bzw. abgeschnitten - der korrekte Terminus dafür ist übrigens Gaußklammern.
Ich zähle nicht nur die Anzahl der Ebenen (Variablen Knoten.Ebene und EbenenInsgesamt), sondern auch die Anzahl der Knoten für jede Ebene (ElementeProEbene[] und ZaehlerProEbene[]) - für diese richte ich mich bei der Größenbemessung der Arrays nach dem theorethischen Maximum an Ebenen und spreche diese über die Indexposition der Arrays an. Die Zählung der Ebenen beginnt bei eins, ein Array aber immer bei null, daher habe ich der Einfachheit halber bei den Größen der Arrays ein einzelnes Element hinzugefügt.
Die Routine für die Visualisierung stammt von mir, ohne Inspiration aus einem Lehrbuch - möglich das es nach akademischen Maßstäben anders realisiert wird, jedoch funktioniert meine Version einwandfrei und ist korrekt. Es wird lediglich bei nur teilweise gefüllten Bäumen der Zwischenabstand zu großzügig berechnet. Die Routine geht davon aus das der Baum maximal gefüllt ist, das entspricht 2^(n-1) Elementen für die Ebene n - und rechnet mit Platzhaltern wenn die Zahl unterschritten wird. Es wird so immer der Abstand von der linken Bildschirmkante berechnet.
Für weitere Erklärungen verweise ich auf die Kommentare im Quellcode weiter unten. Structs kennt es außerdem nicht, ich musste meine erste Version von Structs auf Klassen ummünzen. Übrigens ist Processing nicht so leichtgewichtig wie man vermuten könnte; um die 120 MB nimmt es entpackt an Platz schon ein.
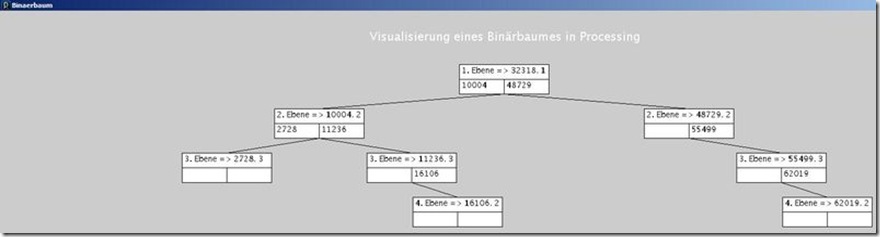
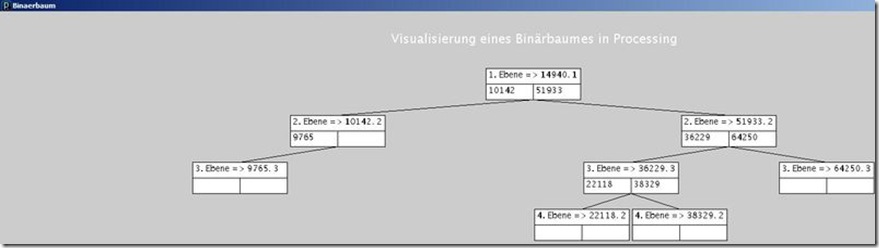
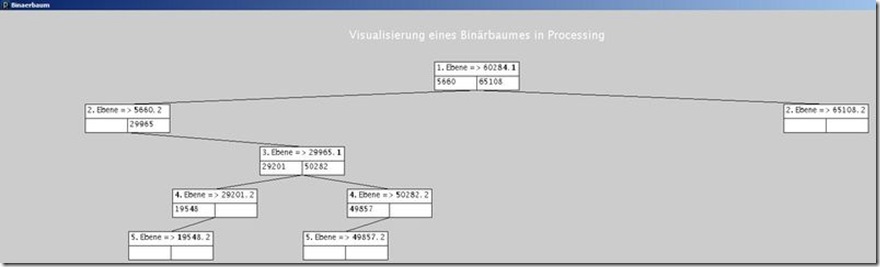
Insgesamt ist Processing für edukative Zwecke sowie Bewerbungs-Projekte gut geeignet. Bitte beachten, das ich unter dem Quellcode noch drei Bilder für die Ausgabe dieses Programms eingefügt habe.
Update 01.05.2011: Ich habe gerade noch einen Fehler korrigiert: In den Bildern unten ist in den Knoten jeweils die Ebene, der Wert des Knotens (Zufallszahl) und nach dem Komma die Anzahl der Knoten auf dieser Ebene eingezeichnet (und darunter der linke und rechte Nachfolger) - in der letzten Ebene war bei den Knoten nach dem Komma immer eine null zu sehen. Das lag daran das die globale Variable Ebene bei null beginnt, aber der Variablen Knoten.Ebene + 1 zugewiesen wurde - es musste also statt ElementeProEbene[Ebene]+=1; ElementeProEbene[Ebene+1]+=1; lauten. Da eben beim Einzeichnen die Anzahl aus dem Array beginnend mit Indexposition eins genommen wird, muss auch beim Inkrementieren des Arrays mit Indexposition eins begonnen werden. In den Bildern wurde so bei den Knoten die Anzahl der Elemente der jeweils nächsten Reihe eingezeichnet - zwischenzeitlich habe ich aber bereits wieder neue Bilder eingefügt.
Update 02.05.2011: Bildschirmzentrierung hinzugefügt – abschaltbar über die globale Variable Zentrierung. Interessant ist das ein Binärbaum subjektiv falsch wirkt, wenn bei der Anzeige keine Zentrierung erfolgt ist. Außerdem habe ich eine Überschrift eingefügt und es werden fortan Linien (Kanten) zwischen den Knoten erzeugt, um die Baumstruktur zu verdeutlichen. Ansonsten ist noch etwas einfacheres Refactoring erfolgt.
Übrigens kennt Processing standardmäßig keine Scrollbalken, der Baum ist somit naturgemäß von der Größe her etwas eingeschränkt - jedenfalls soweit es noch Sinn ergibt. Eigentlich wollte ich auch das ausführbare Programm zum Download anbieten - die Processing für Linux, MacOS und Windows erzeugen kann –, aber beim Einfügen der Datei zeigt BlogEngine.NET immer eine Fehlermeldung an. Somit muss ich das leider schuldig bleiben.
Update 05.05.2011: Wenn die Zentrierung deaktiviert ist greift nun ein anderer Modus - in diesem kann der gesamte Bildschirminhalt (außer den Überschriften) mit der Maus verschoben werden, um möglichst alles vom Baum sehen zu können. Der einfacheren Anwendung halber bleibt der Bereich dabei aber auf das anderthalbfache (jeder Richtung) der Auflösung beschränkt. Zu Testzwecken - und damit man sieht das das Programm nicht abgestürzt ist - wird in dem Modus auch die aktuelle Mausposition oben links eingeblendet.
Update 12.05.2011: Ich habe nun auch Visualisierungs-Algorithmen für Bäume aus dem akademischen Bereich gefunden, wie den Reingold-Tilford-Algorithmus - ich füge entsprechende Quellen unten an. Allerdings wird so etwas vermutlich eher an Universitäten gelehrt, an unserer Fachhochschule wird das gar nicht behandelt (zumindest nicht im Bachelor) - meine Visualisierung erfolgte aus Eigeninitiative.
Dieser Algorithmus wurde übrigens 1981 vorgestellt und ist auf Binärbäume beschränkt - mit dem 1990 vorgestellten Walker-Algorithmus existiert ein anderer Algorithmus, um Bäume von unbeschränktem Grad zu zeichnen.
Mittlerweile habe ich auch den Reingold-Tilford-Algorithmus in Processing implementiert, siehe meinen nachfolgenden Blog-Eintrag.
Weitere Links: Implementierung
- Wikipedia zum Thema Binärer Suchbaum: Link
- Buch Das Ingenieurwissen: Link
- Binärbäume und AVL-Bäume: Link
- Prüfungsfragen samt Lösungen: Link
- Implementierung in C++: Link
- Ein Gymnasium-Referat am Rande: Link
Weitere Links: Visualisierung
- Algorithmen zur Visualisierung von Graphen: Link
- Der Reingold-Tilford-Algorithmus: Link
- Visualisierung sehr großer Graphen: Link
- ViA: Visualisieren von Algorithmen: Link
- Entwicklung und Implementierung einer interaktiven AVL-Animation: Link
/************************************************************************************
Visualisierung eines binären Suchbaumes in Processing
von Thomas Kramer
Version 0.6 - 05.05.2011
************************************************************************************/
/* Konfiguration */
int Baumelemente=12;
// wenn Zentrierung aktiviert wird, werden die Mausabfragen deaktiviert
boolean Zentrierung=false;
/* Zufallszahlen-Unter-/Oberwert */
int unten=1;
int oben=65536;
int AbstandOben=25;
int AbstandLinks=10;
int ZwischenAbstandOben=25;
int ZwischenAbstandLinks=5;
int Breite=150;
int Hoehe=50;
/* Farbe festlegen (schwarz, weiss und hintergrund) */
color c1 = color(0, 0, 0);
color c2 = color(255,255,255);
color c3 = color(193,185,185);
/* Konfiguration-Ende */
int Ebene=0;
int EbenenInsgesamt=0;
int[] Zufallszahlen=new int[Baumelemente+1];
int[] ElementeProEbene=new int[Baumelemente+1];
int[] ZaehlerProEbene=new int[Baumelemente+1];
class tBaum
{
int Inhalt;
int Ebene;
tBaum links;
tBaum rechts;
};
tBaum Wurzel;
void setup() {
/* Größe des Screens setzen */
size(screen.width,screen.height);
background(c3);
/*-----------------------------------------------------------------------------
* Knoten erzeugen
*-----------------------------------------------------------------------------*/
for (int i=1;i<=Baumelemente;i+=1)
{
Zufallszahlen[i]=(int) random(unten,oben);
if (i==1)
{
Wurzel=Einfuegen(null,Zufallszahlen[i]);
} else {
Einfuegen(Wurzel,Zufallszahlen[i]);
}
}
/*-----------------------------------------------------------------------------
* Maus auf Mittelposition setzen (innerhalb des Fensters)
*-----------------------------------------------------------------------------*/
mouseX=(screen.width/2);
mouseY=(screen.height/2)-50;
/*-----------------------------------------------------------------------------
* erneute Aufrufe des Events draw() verhindern
*-----------------------------------------------------------------------------*/
// noLoop();
}
void draw()
{
background(c3);
/*-----------------------------------------------------------------------------
* Überschriften setzen
*-----------------------------------------------------------------------------*/
fill(c2);
textSize(20);
text("Visualisierung eines binären Suchbaumes in Processing",((screen.width)/2)-260,50);
textSize(15);
text("(ESC zum Abbrechen)",((screen.width)/2)-75,80);
textSize(13);
/*-----------------------------------------------------------------------------
* Zähler zurücksetzen, ist für erneute Aufrufe notwendig!
*-----------------------------------------------------------------------------*/
for (int i=0;i<=Baumelemente;i++)
{
ZaehlerProEbene[i]=0;
}
/*-----------------------------------------------------------------------------
* Baum grafisch ausgeben
*-----------------------------------------------------------------------------*/
ZeigeBaum(Wurzel, 0, 0);
/*-----------------------------------------------------------------------------
* aktuelle Mauskoordinaten ausgeben
*-----------------------------------------------------------------------------*/
if (!Zentrierung)
{
fill(c3);
rect(0,0,80,60);
fill(c2);
text("x: " + mouseX,20,20);
text("y: " + mouseY,20,40);
}
}
tBaum Einfuegen(tBaum Knoten, int Inhalt)
{
if (Knoten==null)
{
/* Neuen Knoten erzeugen */
Knoten = new tBaum();
Knoten.links = null;
Knoten.rechts = null;
Knoten.Inhalt = Inhalt;
Knoten.Ebene = Ebene+1;
if ((Ebene+1)>EbenenInsgesamt)
EbenenInsgesamt=(Ebene+1);
ElementeProEbene[Ebene+1]+=1;
/* Zeiger auf neuen Knoten zurückgeben */
return Knoten;
}
Ebene+=1;
if (Inhalt < Knoten.Inhalt)
{
/* kleineren Wert als den des aktuellen Knotens immer als linken Sohn einfügen */
Knoten.links = Einfuegen(Knoten.links, Inhalt);
}
else if (Inhalt > Knoten.Inhalt)
{
/* größeren Wert als den des aktuellen Knotens immer als rechten Sohn einfügen */
Knoten.rechts = Einfuegen(Knoten.rechts, Inhalt);
}
Ebene-=1;
/* gib den aktuellen Knoten zurück */
return Knoten;
}
void ZeigeBaum(tBaum Knoten, int StartPosKanteLinks, int StartPosKanteOben)
{
if (Knoten==null)
return;
int Faktor=0;
float Basis=2;
float Ergebnis=0;
int AbstandLinks2=0;
int GesamtPositionLinks=0;
int GesamtPositionOben=0;
int MaxElemente=(int) exp((EbenenInsgesamt-1)*log(Basis));
int MaxElementePlatz=(MaxElemente*Breite)+((MaxElemente-1)*ZwischenAbstandLinks);
int Zentri_Space=(screen.width-AbstandLinks-MaxElementePlatz)/2;
/* Berechnet den Faktor für die Zwischenabstände. Zwischen der ersten und der letzten
Ebene gibt es zwischen jedem eingefügten Element einen oder mehrere Platzhalter.
Beispiel: Angenommen es gibt fünf Ebenen, dann sind in der letzten Ebene maximal 2^4=16
Elemente vorhanden mit lediglich einem Mindestabstand dazwischen, wenn das Max ausgelastet
wird.
Aber in der Ebene 4 gibt es dann zwischen jedem eingefügten Element zusätzlich einen
Platzhalter (Leerzeichen mit bestimmter Länge, so breit wie ein gezeichnetes Element),
in der 3. Ebene sind es dann zwischen jedem eingefügten Element 3 Platzhalter, in der
2. Ebene 7 usw... Das ist eine mathematische Folge, sie lautet "mal 2 + 1"
Das ist deswegen wichtig weil je mehr Ebenen es gibt desto mehr Platz muss zwischen den
Elementen in den oberen Ebenen gelassen werden, um den Baum korrekt zu zeichnen.
Theorethisch kann der freie Raum noch verringert werden, aber es darf nicht den Anschein
erwecken das ein Element zwei Väter hat.
*/
if (Knoten.Ebene!=EbenenInsgesamt)
{
Faktor=1;
for (int i=1;i<(EbenenInsgesamt-Knoten.Ebene);i++)
Faktor=Faktor*2+1;
}
/* LeereFelder sind die Felder, die zwischen der ersten und der letzten Ebene zwischen jedem
eingefügten Element immer vorhanden sind.
BenutzteFelder enthält die Elemente die gezeichnet werden, aber auch die Platzhalter davon
wenn ein Vorgängerknoten lediglich einen oder keinen Nachfolger hatte.
AbstandLinks2: neben dem grundsätzlichen Abstand zur linken Bildschirmkante (AbstandLinks)
beginnt jede weitere Ebene von unten nach oben ein wenig weiter eingerückt.
Wie gesagt sind die Anzahl Platzhalter pro Ebene von unten nach oben 1, 3, 7, davon
jeweils die Hälfte muss links als Abstand aufaddiert werden.
*/
ZaehlerProEbene[Knoten.Ebene]+=1;
int LeereFelder=(ZaehlerProEbene[Knoten.Ebene]-1)*Faktor*(Breite+ZwischenAbstandLinks);
int BenutzteFelder=(ZaehlerProEbene[Knoten.Ebene]-1)*(Breite+ZwischenAbstandLinks);
if (Knoten.Ebene!=EbenenInsgesamt)
AbstandLinks2=round((Faktor*(Breite+ZwischenAbstandLinks))/2.0);
if (Zentrierung)
{
GesamtPositionLinks=Zentri_Space+AbstandLinks+AbstandLinks2+LeereFelder+BenutzteFelder;
GesamtPositionOben=AbstandOben+(Knoten.Ebene*Hoehe)+(Knoten.Ebene*ZwischenAbstandOben);
} else {
GesamtPositionLinks=((screen.width/2)-mouseX)-AbstandLinks+AbstandLinks2+LeereFelder+BenutzteFelder;
GesamtPositionOben=((screen.height/2)-mouseY)-AbstandOben+(Knoten.Ebene*Hoehe)+(Knoten.Ebene*ZwischenAbstandOben);
}
/* Rahmen zeichnen */
fill(c2);
rect(GesamtPositionLinks,
GesamtPositionOben,
Breite,
Hoehe);
/* Inhalte einzeichnen */
fill(c1);
text(Knoten.Ebene+". Ebene => " +Knoten.Inhalt + ", " + ElementeProEbene[Knoten.Ebene],
GesamtPositionLinks+5,
GesamtPositionOben+15);
line(GesamtPositionLinks,
GesamtPositionOben+(Hoehe/2),
GesamtPositionLinks+Breite,
GesamtPositionOben+(Hoehe/2));
line(GesamtPositionLinks+(Breite/2),
GesamtPositionOben+(Hoehe/2),
GesamtPositionLinks+(Breite/2),
GesamtPositionOben+Hoehe);
if (Knoten.links!=null)
text((Knoten.links).Inhalt,
GesamtPositionLinks+5,
GesamtPositionOben+(Hoehe/2)+15);
if (Knoten.rechts!=null)
text((Knoten.rechts).Inhalt,
GesamtPositionLinks+(Breite/2)+5,
GesamtPositionOben+(Hoehe/2)+15);
if (Knoten.Ebene!=1)
line(StartPosKanteLinks,StartPosKanteOben,GesamtPositionLinks+(Breite/2),GesamtPositionOben);
/* rekursive Funktionsaufrufe, und für den Fall das einer der zwei möglichen Nachfolger
eines Knotens nicht gesetzt ist muss der Zähler der Nachfolger-Ebenen erhöht
werden, entweder vorher (wenn rechter Nachfolger noch gesetzt) oder nachher (linker
Nachfolger noch gesetzt)
*/
if (Knoten.links!=null && Knoten.rechts!=null) {
ZeigeBaum(Knoten.links, GesamtPositionLinks+(Breite/2), GesamtPositionOben+Hoehe);
ZeigeBaum(Knoten.rechts, GesamtPositionLinks+(Breite/2), GesamtPositionOben+Hoehe);
} else
{
if (Knoten.links==null && Knoten.rechts==null)
{
for (int Exponent=1;Exponent<=(EbenenInsgesamt-Knoten.Ebene);Exponent++)
{
Ergebnis=exp(Exponent*log(Basis));
ZaehlerProEbene[Knoten.Ebene+Exponent]+=Ergebnis;
}
} else
{
if (Knoten.rechts==null)
ZeigeBaum(Knoten.links, GesamtPositionLinks+(Breite/2), GesamtPositionOben+Hoehe);
for (int Exponent=0;Exponent<=(EbenenInsgesamt-Knoten.Ebene-1);Exponent++)
{
Ergebnis=exp(Exponent*log(Basis));
ZaehlerProEbene[Knoten.Ebene+1+Exponent]+=Ergebnis;
}
if (Knoten.links==null)
ZeigeBaum(Knoten.rechts, GesamtPositionLinks+(Breite/2), GesamtPositionOben+Hoehe);
}
}
}